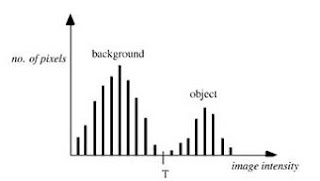
Esta técnica de umbralización
supone que la imagen posee un histograma bimodal, y por lo tanto, el objeto
puede ser extraído del resto de la imagen mediante una simple operación que
compare los valores de la imagen con el valor umbral T.
Fig. 1: Histograma bimodal con umbral T.
Para una imagen f(x,y), con el histograma de la figura 1,
los píxeles del objeto y del fondo tienen los niveles de gris agrupados en dos
modos dominantes. La manera más obvia de extraer el objeto es seleccionar un
umbral T que separe los dos modos.
La imagen g(x,y), resultante de aplicar la umbralización, viene definida por:
El resultado es una imagen
binaria, donde los píxeles con valores de intensidad igual a 1 corresponden al
objeto deseado; mientras que los píxeles con valor 0, corresponder al resto de
la imagen.
La figura 2 muestra el
resultado de la segmentación de una imagen mediante umbralización, donde la
imagen original 2(a) contiene células blancas sobre un fondo negro, y las
intensidades de los píxeles varían entre 0 y 255. El umbral T=127 se selecciona
como el mínimo entre los dos modos del histograma 2(b), y el resultado de la
segmentación se muestra en la figura 2(c), donde los píxeles con
intensidades que superen el umbral (T=127) se representan en blanco. En última
instancia, en la figura 2(d), los bordes de las células se obtienen
aplicando el laplaciano de orden tres
a la imagen umbralizada (figura 2c).
Fig. 2: (a)
Imagen original, (b) histograma de la imagen, (c) resultado de la umbralización
con T=127, y (d) bordes de las células.
Hay muchas maneras para
seleccionar un umbral global, una de ellas se basa en un modelo de
clasificación que minimice la probabilidad de error. Por ejemplo, para el caso
de una imagen con un histograma bimodal, se puede calcular el error como el
número total de píxeles del fondo que se clasifican como del objeto, y píxeles
del objeto que se clasifican en el fondo. Una versión semiautomatizada de esta
técnica, para medir volúmenes ventriculares de resonancia magnéticas en 3D;
consiste en que un operador selecciona manualmente dos píxeles, uno del objeto
y otro del fondo. Comparando la distribución de las intensidades de píxel en
regiones circulares alrededor de los píxeles seleccionados, se calcula
automáticamente el umbral y se corresponde con el mínimo número de píxeles mal
clasificados entre las dos regiones. El resultado es de esta técnica se muestra
como un mapa del contorno, superpuesto a la imagen original. Además, en caso
que fuera necesario, el operador puede modificar manualmente cualquier parte
del borde. Esta misma técnica también se aplicó para extraer linfomas de
imágenes CT, pero se encontró muy dependiente de la selección de los puntos interiores y exteriores por parte
del usuario.
En muchas aplicaciones se
obtiene una segmentación apropiada cuando el área, o perímetro, de los objetos,
es sensible a pequeñas variaciones del nivel umbral seleccionado. En la figura 3(a)
se muestra el perfil de intensidad de un objeto que es más brillante que el
fondo, y tres umbrales (T1, T2
y T3) para llevar a cabo la segmentación. Una pequeña variación ΔT, en el nivel umbral más bajo,
causaría cambios significativos en el área, o perímetro, del objeto segmentado;
esto mismo se da, también, para el nivel umbral más alto. En cambio, una
variación ΔT en el nivel umbral
medio, tendría una mínima influencia sobre el área, o perímetro, del objeto.
Fig. 3: (a)
Histograma con umbrales T1, T2 y T3, y (b) representación gráfica del área o el
perímetro frente al umbral T.
El área A(T) y el perímetro P(T),
son funciones que dependen del umbral T, y suelen presentar un aspecto similar
al de la figura 3(b). Por lo tanto, el umbral que minimiza dA(T)/dT y dP(T)/dT, es una buena opción, especialmente ante la ausencia de un
operador manual, y/o no se dispone de información previa del objeto.
Una técnica relaciona que evalúa
múltiples umbrales, está basada en la estimación del valor del gradiente en el
contorno del objeto segmentado. El valor medio del gradiente medio viene dado
por:
donde H(T) es la función de histograma. El umbral que
maximiza el límite del gradiente medio es el que se selecciona.
Si una
imagen contiene más de dos tipos de regiones, es posible segmentarla usando
varios umbrales simples, o usando la técnica
de umbrales múltiples. Con el incremento del número de regiones, aumenta el
número de modos a distinguir dentro del histograma; y por lo tanto, la
selección del umbral se vuelve más difícil.
El uso de
umbrales globales es computacionalmente más simple y rápido. Funciona bien con
imágenes que contienen objetos con una intensidad uniforme, y diferenciados del
fondo. Sin embargo, falla si existe un bajo contraste entre el objeto y el
fondo, si la imagen es ruidosa, o si la intensidad del fondo varía
significativamente a lo largo de la imagen.
.gif)
